Continuous Bijection Not Homeomorphism Fixed Point

1. Introduction

A paper [1] (resp. [2]) explored some features of

$({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$

(resp. Khalimsky line) and newly proposed two topologies derived from quotient spaces of the one point compactification of

$({\mathbb{Z}}^2,\gamma )$

(resp. Khalimsky line). Based on the work, the present paper continues the study of

$({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$

from the viewpoint of fixed point theory and finally addresses a certain unsolved problem already mentioned in abstract.

From now on the term "Marcus-Wyse" will be often replaced with "

$M$

-" for brevity. We shall also use the symbol "

$:=$

" to define new terminology. In a category

$\mathcal{C}$

, let us recall that an object

$X(\in Ob(\mathcal{C}\left)\right)$

has the fixed point property (FPP) if for every self-morphism

$f(\in Mor(\mathcal{C}\left)\right)$

of X, there is an element

$x\in X$

such that

$f\left(x\right)=x$

. After establishing a certain category relating to the Alexandroff compactification of the M-topological plane, we address the unsolved problem: Under what category does

$({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$

have the fixed point property (FPP, for short) ? Regarding this work, we need some new ideas and tools.

Let us now recall some terminology which will be used later in the paper. We usually denote by

$({\mathbb{Z}}^2,\gamma )$

the M-topological plane (see Section 2), where

$\gamma$

is the topological structure of

${\mathbb{Z}}^2$

generated by a special kind of set as a base (see (1) and (2) for the details). As usual, we often denote by

${\aleph }_0$

the first infinite cardinal number. Besides,

$|·|$

means the cardinality of a given set, and we denote by

$\mathbb{N}$

the set of natural numbers. As usual, a topological space

$(X,T)$

is called locally compact [3] if for each point

$x\in X$

there is a compact neighborhood containing the point x. It is obvious that the M-topological space

$({\mathbb{Z}}^2,\gamma )$

is neither a Hausdorff nor a compact space but it is a locally compact space (see later in Section 2 for the details). Hence we can establish the Alexandroff one point compactification of

$({\mathbb{Z}}^2,\gamma )$

and further, we call it the infinite M-topological sphere [3]. Hereafter, we denote by

$({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$

the one point compactification of

$({\mathbb{Z}}^2,\gamma )$

[1].

To study the FPP of

$({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$

, we need to define the following category.

Definition1.

We denote by $Mop\left({\gamma }^{\ast }\right)$ the category whose object is the only $({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$ and morphisms are all continuous self-maps g of $({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$ such that $|g\left({\left({\mathbb{Z}}^2\right)}^{\ast }\right)|={\aleph }_0$ with $\ast \in g\left({\left({\mathbb{Z}}^2\right)}^{\ast }\right)$ or $g\left({\left({\mathbb{Z}}^2\right)}^{\ast }\right)$ is a singleton.

The present paper disproves the FPP of the infinite M-topological sphere in

$Con({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast }))$

which denotes the set of all continuous self-maps of the infinite M-topological sphere (see Theorem 2). Hence we need to establish a suitable subcategory of it having the FPP. Although, in general, a continuous bijection need not imply a homeomorphism, we wonder if a continuous self-bijection of

$({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$

is a homeomorphism. Thus we may raise the following queries.

(1-1) Does any continuous self-map g of

$({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$

have a point x in

${\left({\mathbb{Z}}^2\right)}^{\ast }$

such that

$g\left(x\right)=x$

?

(1-2) Is a continuous self-bijection of

$({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$

equivalent to a self-homeomorphism of it?

(1-3) Under what category does

$({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$

have the FPP?

(1-4) Does

$({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$

have the FPP in the category

$Mop\left({\gamma }^{\ast }\right)$

?

(1-5) What category is the maximal one with respect to the inclusion relation which admits the FPP of

$({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$

?

The present paper suggests some affirmative solutions to the queries (1-2), (1-3), and (1-4) and answers to the query of (1-1) negatively. In view of these facts, comparing with the non-FPP of the Hausdorff compactifications of the 2-dimensional usual topological space, we can recognize the study of the FPP of

$({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$

has its own feature.

The remainder of the paper is organized as follows: Section 2 deals with some notions related to the M-topology and the Alexandroff compactification. Section 3 investigates various properties of continuous self-maps (or surjections or bijections) of

$({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$

. Section 4 proves that every morphism g of

$Mop\left({\gamma }^{\ast }\right)$

has some point

$x\in {\left({\mathbb{Z}}^2\right)}^{\ast }$

such that

$g\left(x\right)=x$

. Section 5 concludes the paper with some remarks and further work.

2. Preliminaries

A topological space

$(X,T)$

is called an Alexandroff space if each point

$x\in X$

has the smallest open set in

$(X,T)$

[4]. Indeed, it is obvious that the usual topological space

$({\mathbb{R}}^n,U)$

is not an Alexandroff space. As an Alexandroff topological space [4,5], the M-topological space was proposed [6] and the study of various properties of it includes the papers [1,6,7,8,9,10,11,12,13]. Regarding digital spaces [14] in

${\mathbb{Z}}^2$

, we will follow the concept of a digital k-neighborhood of a point

$p\in {\mathbb{Z}}^2$

.

For a point

$p:=(x,y)\in {\mathbb{Z}}^2$

we follow the notation [15].

$$N_4\left(p\right):=\{(x\pm 1,y),p,(x,y\pm 1)\}\subset {\mathbb{Z}}^2,$$

Then we use the set

$U\left(p\right)$

developing the M-topology on

${\mathbb{Z}}^2$

, where

$$U\left(p\right):=\left\{\begin{array}{l}{N}_4\left(p\right)\mathrm{if}x+y\mathrm{is}\mathrm{even},\mathrm{and}\\ \left\{p\right\}:\mathrm{otherwise}.\end{array}\right\}$$

(1)

The M-topology "

$\gamma$

" on

${\mathbb{Z}}^2$

is derived from the set

$\left\{U\left(p\right)\right|p=(x,y)\in {\mathbb{Z}}^2\}$

in (1) as a base [6]. Then we use the notation

$({\mathbb{Z}}^2,\gamma )$

for the topological space. To further state a point in

${\mathbb{Z}}^2$

, we call a point

$p=(x_1,x_2)$

double even if

$x_1+x_2$

is an even number such that each

$x_i$

is even,

$i\in \{1,2\}$

; even if

$x_1+x_2$

is an even number such that each

$x_i$

is odd,

$i\in \{1,2\}$

; and odd if

$x_1+x_2$

is an odd number [6].

In a subspace of

$({\mathbb{Z}}^2,\gamma )$

, an odd point (resp. a double even point or even point) is denoted by a black large dot (resp. the symbol ◊). According to (1), under

$({\mathbb{Z}}^2,\gamma )$

, it appears that the singleton being composed of "

$◊$

" is a closed set and the singleton consisting of a black large dots is an open set. Besides, we will denote by

${\left({\mathbb{Z}}^2\right)}_O$

(resp.

${\left({\mathbb{Z}}^2\right)}_E$

) the set of all odd points (resp. double even or even points) in

$({\mathbb{Z}}^2,\gamma )$

. In addition, for a set

$X\subset {\mathbb{Z}}^2$

, we denote by

$(X,{\gamma }_X)$

, called an M-topological space, the subspace induced by

$({\mathbb{Z}}^2,\gamma )$

. Owing to (1), it is obvious that

$({\mathbb{Z}}^2,\gamma )$

is an Alexandroff space.

Under

$({\mathbb{Z}}^2,\gamma )$

, the smallest (open) neighborhood of the point

$p:=(p_1,p_2)$

of

${\mathbb{Z}}^2$

, denoted by

$S{N}_M\left(p\right)\subset {\mathbb{Z}}^2$

, is determined according to the given point p, as follows:

$$S{N}_M\left(p\right):=\left\{\begin{array}{l}\left\{p\right\}\mathrm{if}p\in {\left({\mathbb{Z}}^2\right)}_O,\\ N_4\left(p\right)\mathrm{if}p\in {\left({\mathbb{Z}}^2\right)}_E.\end{array}\right\}$$

(2)

From now on, for a point p in

$(X,{\gamma }_X)$

, we follow the notation

$S{N}_X\left(p\right):=S{N}_M\left(p\right)\cap X$

or

$V\left(p\right)$

[7]. Owing to (2),

$(X,{\gamma }_X)$

is obviously a locally finite topological space.

According to the property (2), the following properties are obtained in

$({\mathbb{Z}}^2,\gamma )$

:

Lemma1.

(1) A subset D of $({\mathbb{Z}}^2,\gamma )$ is open [1] if and only if

$$N_4\left(p\right)\backslash \left\{p\right\}\subset D\mathit{whenever}p\in D,\mathit{where}p\in \{(2m,2n),(2m+1,2n+1)|m,n\in \mathbb{Z}\}.$$

(2) A subset C of $({\mathbb{Z}}^2,\gamma )$ is closed if and only if $N_4\left(q\right)\backslash \left\{q\right\}\subset C$ whenever $q\in C$, where $q\in \left\{\right(2m+1,2n),(2m,2n+1\left)\right|m,n\in \mathbb{Z}\}.$

By Lemma 1 and the property (2), under

$({\mathbb{Z}}^2,\gamma )$

, we obtain the following: For the point

$q\in {\left({\mathbb{Z}}^2\right)}_O$

,

$Cl\left(\right\{q\left\}\right)$

can be represented as follows:

$$Cl\left(S{N}_M\left(q\right)\right)=Cl\left(\left\{q\right\}\right)=N_4\left(q\right),$$

(3)

where "

$Cl$

" means the closure operator.

Owing to (1),

$({\mathbb{Z}}^2,\gamma )$

is locally compact but neither compact nor Hausdorff. To be specific, let us check that

$({\mathbb{Z}}^2,\gamma )$

is not Hausdorff. To be precise, under the M-topological space

$({\mathbb{Z}}^2,\gamma )$

, take two distinct points

$p:=(0,0),q:=(1,0)$

. Then we see that no open sets

$U,V\in \gamma$

exist such that

$p\in U$

,

$q\in V$

and

$U\cap V=\varnothing$

because the smallest open set

$U(\ni p)$

is

$\left\{\right(\pm 1,0),p,(0,\pm 1\left)\right\}$

and the smallest open set

$V(\ni q)$

is the singleton

$\left\{q\right\}$

(see Section 2 for the details), i.e.,

$V\subset U$

, which implies that

$({\mathbb{Z}}^2,\gamma )$

is not Hausdorff.

Next, we now check the non-compactness of

$({\mathbb{Z}}^2,\gamma )$

. Let

$$\left\{\begin{array}{l}C:=\{N_4\left(p\right):=\{(p_1\pm 1,p_2),p,(p_1,p_2\pm 1)\},\mathrm{where}\\ p:=(p_1,p_2)\in \{(2m,2n),(2m+1,2n+1)|m,n\in \mathbb{Z}\}.\end{array}\right\}$$

Though C is an open covering for

$({\mathbb{Z}}^2,\gamma )$

with

$C^{♯}={\aleph }_0$

, a deletion of at least one element from C does not support a covering of

${\mathbb{Z}}^2$

, which implies that

$({\mathbb{Z}}^2,\gamma )$

is not compact. Finally, since any point

$p\in ({\mathbb{Z}}^2,\gamma )$

has an smallest open set which is compact, it turns out that

$({\mathbb{Z}}^2,\gamma )$

is locally compact. Thus we can proceed with the Alexandroff compactification of

$({\mathbb{Z}}^2,\gamma )$

[3], denoted by

$({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$

.

To be specific, take a certain object outside X, denoted by the symbol

$\ast (\mathrm{or}\infty )\notin X$

, and add it to X, creating the set

$X^{\ast }:=X\cup \{\ast \}$

[4]. Topologize

$X^{\ast }$

using the following sets as open sets '

$O$

' in

$X^{\ast }$

.

$(\ast 1)$ $O(\in T)$

$(\ast 2)$ $O(\ni \ast )\subset X^{\ast }$

, where

$O^c$

is a closed and compact subset of

$(X,T)$

, and

$O^c$

means the complement of the set O in

$X^{\ast }$

.

This topological space is called the Alexandroff one-point compactification of

$(X,T)$

and denoted by

$(X^{\ast },T^{\ast })$

.

Taking this approach, we obtain

$({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$

from

$({\mathbb{Z}}^2,\gamma )$

which will be often called the infinite M-topological sphere [1]. In

$({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$

, it appears that

$$\left\{\begin{array}{l}Cl\left({\mathbb{Z}}^2\right)={\left({\mathbb{Z}}^2\right)}^{\ast }\mathrm{and}\mathrm{further},\\ Cl\left(\{\ast \}\right)=\{\ast \}\mathrm{but}\{\ast \}\mathrm{is}\mathrm{not}\mathrm{an}\mathrm{open}\mathrm{set}\mathrm{of}({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast }).\end{array}\right\}$$

Besides, under

$({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$

, we need to remind that for an open set, say O, containing the point ∗,

$O^c$

is a closed and compact set of

$({\mathbb{Z}}^2,\gamma )$

. Owing to the property (2), it appears that

$$\mathrm{an}\mathrm{infinite}\mathrm{subset}\mathrm{of}({\mathbb{Z}}^2,\gamma )\mathrm{is}\mathrm{not}\mathrm{compact}\mathrm{in}({\mathbb{Z}}^2,\gamma ),$$

(4)

and further, for an open set

$O(\in {\gamma }^{\ast }\backslash \gamma )$

,

$O^c$

should be finite and closed in

$({\mathbb{Z}}^2,\gamma )$

.

Proposition1.

Under $({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$, we obtain the following:

(1) ${\left({\mathbb{Z}}^2\right)}^{\ast }\backslash A$ is closed but is not compact, where A is a countable subset of ${\left({\mathbb{Z}}^2\right)}_O$.

(2) ${\left({\mathbb{Z}}^2\right)}^{\ast }\backslash B$ is not open, where B is a denumerable subset of ${\left({\mathbb{Z}}^2\right)}_E$.

Proof.

(1) It is clear that

${\left({\mathbb{Z}}^2\right)}^{\ast }\backslash \left\{o\right\}$

is closed, where

$o\in {\left({\mathbb{Z}}^2\right)}_O$

. Obviously, the set

${\left({\mathbb{Z}}^2\right)}^{\ast }\backslash A$

is an intersection of the closed sets

${\left({\mathbb{Z}}^2\right)}^{\ast }\backslash \left\{o_i\right\},o_i\in {\left({\mathbb{Z}}^2\right)}_O,i\in M$

and M is a countable set. Thus the proof is completed.

Owing to (4), the set

${\left({\mathbb{Z}}^2\right)}^{\ast }\backslash A$

is not compact in

$({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$

because it is denumerable.

(2) Let us consider the set

$B:=\left\{4m\right|m\in \mathbb{Z}\}$

in

$({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$

. Whereas it is closed in

$({\mathbb{Z}}^2,\gamma )$

, it is not compact in

$({\mathbb{Z}}^2,\gamma )$

, which proves the assertion. □

In view of Proposition 1(2), we obtain the following:

Corollary1.

${\left({\mathbb{Z}}^2\right)}^{\ast }\backslash {\left({\mathbb{Z}}^2\right)}_E$ is not open.

Proof.

Though

${\left({\mathbb{Z}}^2\right)}_E$

is closed in

$({\mathbb{Z}}^2,\gamma )$

, it is not compact in

$({\mathbb{Z}}^2,\gamma )$

, which completes the proof. □

Remark1.

$({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$ is connected.

Proof.

According to the definition of

$({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$

, we obtain

${\mathbb{Z}}^2\subset {\left({\mathbb{Z}}^2\right)}^{\ast }=Cl\left({\mathbb{Z}}^2\right)$

. Owing to both the connectedness of

$({\mathbb{Z}}^2,\gamma )$

and this property lead to the connectedness of

$({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$

. □

For two spaces

$X:=(X,{\gamma }_X)$

and

$Y:=(Y,{\gamma }_Y)$

, a map

$g:X\to Y$

is said to be M-continuous at a point

$x\in X$

if g is continuous at the point x from the viewpoint of M-topology. Furthermore, we say that a map

$g:X\to Y$

is M-continuous if it is M-continuous at every point

$x\in X$

. Indeed, since

$({\mathbb{Z}}^2,\gamma )$

is an Alexandroff space (see the property (1)), we can represent the M-continuity of g at a point

$x\in X$

[7], as follows:

$$g\left(S{N}_M\left(x\right)\right)\subset S{N}_M\left(g\left(x\right)\right).$$

(5)

In addition, for two spaces

$(X,{\gamma }_X)$

and

$(Y,{\gamma }_Y)$

, a map

$h:X\to Y$

is called an M-homeomorphism if h is an M-continuous bijection and further,

$h^{-1}:Y\to X$

is M-continuous.

3. Continuous Self-Maps of $({\left({\mathbb{Z}}^{\mathbf{2}}\right)}^{\ast },{\mathbf{\gamma }}^{\ast })$

Let us now consider continuous self-bijections of

$({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$

which can play important roles in Section 4 (see Theorem 2).

Remark2.

The followings are continuous self-bijections of

$({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$

.

$$\left\{\begin{array}{l}{g}^{\ast }\left((x,y)\right)=(x+2m+1,y+2n+1),(x,y)\in {\mathbb{Z}}^2,m,n\in \mathbb{Z},\mathrm{and}\\ g^{\ast }(\ast )=\ast .\\ f^{\ast }\left((x,y)\right)=(x+2m,y+2n),(x,y)\in {\mathbb{Z}}^2,m,n\in \mathbb{Z},\mathrm{and}\\ f^{\ast }(\ast )=\ast .\end{array}\right\}$$

Proof.

(1) Given the self-bijection

$g^{\ast }$

of

$({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$

, for any point

$p:=(x,y)\in {\mathbb{Z}}^2$

, we obviously have the following cases.

(Case 1) For any point

$p\in {\mathbb{Z}}^2$

and the smallest open set

$S{N}_M\left(g^{\ast }\left(p\right)\right)$

in

$\gamma$

, we have

$S{N}_M\left(p\right)$

in

$\gamma$

such that

$S{N}_M\left(p\right)={\left(g^{\ast }\right)}^{-1}\left(S{N}_M\left(g^{\ast }\left(p\right)\right)\right)$

. Then this open set

$S{N}_M\left(p\right)$

supports the continuity of

$g^{\ast }$

at the point p (see the property (1)).

(Case 2) For the point

$\ast \in {\left({\mathbb{Z}}^2\right)}^{\ast }$

and any open neighborhood of

$g^{\ast }(\ast )$

, denoted by

$O_M\left(g^{\ast }(\ast )\right)$

, we have an open neighborhood of ∗, denoted by

$O_M(\ast )$

in

${\gamma }^{\ast }$

, such that

$O_M(\ast )={\left(g^{\ast }\right)}^{-1}\left(O_M\left(g^{\ast }(\ast )\right)\right)$

because we may take the open sets

$O_M(\ast )$

and

$O_M\left(g^{\ast }(\ast )\right)$

such that

$$\left\{\begin{array}{l}|O_M(\ast )|={\aleph }_0=|O_M\left(g^{\ast }(\ast )\right)|\\ \mathrm{both}{\left({\mathbb{Z}}^2\right)}^{\ast }\backslash O_M(\ast )\mathrm{and}{\left({\mathbb{Z}}^2\right)}^{\ast }\backslash O_M\left(g^{\ast }(\ast )\right)\mathrm{are}\mathrm{compact}\mathrm{and}\mathrm{closed}\mathrm{in}({\mathbb{Z}}^2,\gamma ),\mathrm{and}\\ |{\left({\mathbb{Z}}^2\right)}^{\ast }\backslash O_M\left(g^{\ast }(\ast )\right)|=|{\left({\mathbb{Z}}^2\right)}^{\ast }\backslash O_M(\ast )|⪇{\aleph }_0.\end{array}\right\}$$

At the moment, we need to mention that the open set

$O_M\left(g^{\ast }(\ast )\right)$

(resp.

$O_M(\ast )$

) is not a minimal open set of the corresponding point

$g^{\ast }(\ast )$

(resp. ∗) because both the points ∗ and

$g(\ast )$

do not have their smallest open neighborhoods in

$({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$

(for the details, see the proof of Lemma 3 and Corollary 4 in the present paper).

(2) Using a method similar to the proof of (1), we complete the proof. □

Lemma2.

A continuous self-map g of $({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$ such that $g(\ast )=p\in {\mathbb{Z}}^2$ is not injective.

Proof.

Assume a continuous self-map g of

$({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$

such that

$g(\ast )=p\in {\mathbb{Z}}^2$

. Take the smallest open neighborhood of the point p, i.e.,

$S{N}_M\left(p\right)$

. Since the set

$$g^{-1}\left(S{N}_M\left(p\right)\right)(\ni \ast )\mathrm{is}\mathrm{an}\mathrm{open}\mathrm{set}\mathrm{in}{\gamma }^{\ast },$$

(6)

it has an infinite cardinality because

$${\left({\mathbb{Z}}^2\right)}^{\ast }\backslash g^{-1}\left(S{N}_M\left(p\right)\right)={\mathbb{Z}}^2\backslash g^{-1}\left(S{N}_M\left(p\right)\right)\mathrm{is}\mathrm{compact}\mathrm{in}({\mathbb{Z}}^2,\gamma ),$$

(7)

which implies that the set

${\left({\mathbb{Z}}^2\right)}^{\ast }\backslash g^{-1}\left(S{N}_M\left(p\right)\right)$

of (7) should be finite (see the property (4)). Hence we should have

$|g^{-1}\left(S{N}_M\left(p\right)\right)|={\aleph }_0$

. Thus the map g should not be injective because

$S{N}_M\left(p\right)$

is finite for any point

$p\in ({\mathbb{Z}}^2,\gamma )$

. □

Let us now investigate a relation between a continuous self-bijection of

$({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$

and a self-homeomorphism of

$({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$

.

Theorem1.

A continuous self-bijection of $({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$ is a homeomorphism.

Proof.

Owing to Lemma 2, every continuous self-bijection g of

$({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$

has the property

$$\left\{\begin{array}{l}g(\ast )=\ast \mathrm{and}\\ g\left(S{N}_M\left(p\right)\right)=S{N}_M\left(g\left(p\right)\right)\mathrm{with}|S{N}_M\left(p\right)|=|S{N}_M\left(g\left(p\right)\right)|,\end{array}\right\}$$

(8)

where

$S{N}_M\left(p\right)$

,

$S{N}_M\left(g\left(p\right)\right)\in \gamma$

.

Next, using a method similar to the approach of Remark 2 (Case 1), for the point

$\ast \in {\left({\mathbb{Z}}^2\right)}^{\ast }$

and each open neighborhood of

$g(\ast )$

, denoted by

$O_M\left(g(\ast )\right)$

, we have an open neighborhood of ∗, denoted by

$O_M(\ast )$

, such that

$$O_M(\ast )=g^{-1}\left(O_M\left(g(\ast )\right)\right).$$

At the moment, we need to mention that the open neighborhood of

$g(\ast )$

(resp. ∗) such as

$O_M\left(g(\ast )\right)$

(resp.

$O_M(\ast )$

) is not minimal open sets of the corresponding points because the points ∗ and

$g(\ast )$

do not have their minimal open neighborhoods in

$({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$

. Thus the inverse of the given continuous self-bijection g of

$({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$

also has the property

$$|S{N}_M\left(q\right)|=|S{N}_M\left(g^{-1}\left(q\right)\right)|\mathrm{and}{g}^{-1}(\ast )=\ast ,$$

where

$q\in {\mathbb{Z}}^2$

. Thus, the given map g should be a homeomorphism. □

In view of Lemma 2 and Theorem 1, we obtain the following:

Corollary2.

A self-homeomorphism g of $({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$ has the property $g(\ast )=\ast$.

As a result, if we consider the category,

$Homeo\left({\gamma }^{\ast }\right)$

, whose object is the only

$({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$

and morphisms are all self-homeomorphisms of it. Then

$({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$

has the FPP in

$Homeo\left({\gamma }^{\ast }\right)$

.

4. The Fixed Point Property of $({\left({\mathbb{Z}}^{\mathbf{2}}\right)}^{\ast },{\mathbf{\gamma }}^{\ast })$ in the Category $\mathit{Mop}\left({\mathbf{\gamma }}^{\ast }\right)$

In view of Theorem 1 and Corollary 2, we may wonder if every continuous self-map g of the space

$({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$

has some point

$x\in {\left({\mathbb{Z}}^2\right)}^{\ast }$

such that

$g\left(x\right)=x$

. A recent paper [1] proved that

$({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$

has the FPP in the category of continuous self-bijections of the space. In view of this result, this section proves that

$({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$

does not have the FPP (see Theorem 1 below), which answers to the query (1-1). It also addresses the queries (1-3) and (1-4) previously posed in Section 1. Let

$Con({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$

be the category whose object is the singleton consisting of

${\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$

and morphisms is the set of all continuous self-maps of

$({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$

. Namely, after firstly proving the non-FPP of

$({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$

, we secondly find a certain subcategory of the category of

$Con({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$

which admits the FPP in the category. This section mainly focuses on establishing a category in which the FPP of

$({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$

holds. Eventually, we prove that every morphism g of

$({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$

in the category

$Mop\left({\gamma }^{\ast }\right)$

has a point

$x\in {\left({\mathbb{Z}}^2\right)}^{\ast }$

such that

$g\left(x\right)=x$

(see Theorem 3). This is a positive answer to the question in [1] such as "Under what condition does

$({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$

have the FPP ?". Let us now address the query (1-1) in Section 1.

Theorem2.

$({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$ does not have the FPP in $Con({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$.

Proof.

Using a counterexample, we prove this assertion. With

$({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$

, consider the self-map g of

${\left({\mathbb{Z}}^2\right)}^{\ast }$

satisfying the following properties of (1-1) and (1-2):

(1-1)

$g\left({\left({\mathbb{Z}}^2\right)}^{\ast }\right)=S{N}_M\left(q\right)=\{(q_1\pm 1,q_2),q,(q_1,q_2\pm 1)\}\subset {\mathbb{Z}}^2$

, where

$q:=(q_1,q_2)\in {\left({\mathbb{Z}}^2\right)}_E$

and further,

(1-2) for

$p:=(p_1,p_2)\in {\left({\mathbb{Z}}^2\right)}_E$

with

$p\ne q$

(see the map g of Figure 1)

$$\left\{\begin{array}{l}g({\left({\mathbb{Z}}^2\right)}^{\ast }\backslash S{N}_M\left(p\right))=\left\{q\right\},\\ g\left(p_i\right)=q_i,i\in \{1,2\},\mathrm{and}\\ g(p_1\pm 1)=q_1\pm 1,g(p_2\pm 1)=q_2\pm 1.\end{array}\right\}$$

(9)

Then the map g is continuous because for the closed singleton

$\left\{q\right\}$

$$g^{-1}\left(\left\{q\right\}\right)=({\left({\mathbb{Z}}^2\right)}^{\ast }\backslash S{N}_M\left(p\right))\cup \left\{q\right\}$$

is closed in

${\gamma }^{\ast }$

and further, the inverse image of any smallest open subset

$S{N}_M\left(q\right)$

by g is also open in

${\gamma }^{\ast }$

. Then we observe that the map g does not have a point

$x\in ({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$

such that

$g\left(x\right)=x$

. □

According to Theorem 2, we have the following:

Corollary3.

Consider the continuous self-map g of $({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$ such that

$$|g\left({\left({\mathbb{Z}}^2\right)}^{\ast }\right)|⪇{\aleph }_0,\mathit{and}\ast \notin g\left({\left({\mathbb{Z}}^2\right)}^{\ast }\right).$$

Then not every map g of $({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$ has a point $x\in {\left({\mathbb{Z}}^2\right)}^{\ast }$ such that $g\left(x\right)=x$.

To address the queries (1-3) and (1-4) in Section 1, we need the following lemmas:

Lemma3.

([1]) In $({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$, the point ∗ does not have an open set $U(\ni \ast )$ that is homeomorphic to $S{N}_M\left(p\right)$, where $p\in {\mathbb{Z}}^2$.

Owing to Lemma 3, we have the following:

Corollary4.

$({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$ is not an Alexandroff space.

Owing to Remark 1 and the definition of

$({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$

, we have the following:

Lemma4.

There is no continuous self-map g of $({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$ such that

$$\left\{\begin{array}{l}2\le |g\left({\left({\mathbb{Z}}^2\right)}^{\ast }\right)|⪇{\aleph }_0,\mathit{and}\\ \ast \in g\left({\left({\mathbb{Z}}^2\right)}^{\ast }\right).\end{array}\right\}$$

(10)

Proof.

Suppose a continuous self-map g of the

$({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$

satisfying the property (10). Then we have the following properties of g:

$$\left\{\begin{array}{l}\left(a\right)g\left({\left({\mathbb{Z}}^2\right)}^{\ast }\right)\mathrm{is}\mathrm{connected},\\ \left(b\right)g\left({\left({\mathbb{Z}}^2\right)}^{\ast }\right)(\ne \varnothing )\mathrm{is}\mathrm{not}\mathrm{an}\mathrm{open}\mathrm{set}\mathrm{in}({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast }),\mathrm{and}\\ \left(c\right)g\left({\left({\mathbb{Z}}^2\right)}^{\ast }\right)\mathrm{does}\mathrm{not}\mathrm{include}\mathrm{any}\mathrm{non}\text{-}\mathrm{trivial}\mathrm{open}\mathrm{set}\mathrm{in}\gamma .\end{array}\right\}$$

(11)

To be precise, owing to Remark 1 and the continuity of g, we obtain the property (a). Owing to the hypothesis of (10), the complement of

$g\left({\left({\mathbb{Z}}^2\right)}^{\ast }\right)$

in

${\left({\mathbb{Z}}^2\right)}^{\ast }$

is denumerable. Thus

$g\left({\left({\mathbb{Z}}^2\right)}^{\ast }\right)$

is not open in

$({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$

. Hence we have the property (b) because

${\left({\mathbb{Z}}^2\right)}^{\ast }\backslash g\left({\left({\mathbb{Z}}^2\right)}^{\ast }\right)$

is not compact in

$({\mathbb{Z}}^2,\gamma )$

. Using a method similar to the proof of (b), we obviously have the property (c). Finally, according to the property (11), we conclude that

$g\left({\left({\mathbb{Z}}^2\right)}^{\ast }\right)$

should be an empty set, which invokes a contradiction of being a map of g. □

According to Lemma 4, it turns out that the map g satisfying the hypothesis of (10) is not a continuous self-map of

$({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$

. Besides, the case

$$g\left({\left({\mathbb{Z}}^2\right)}^{\ast }\right)\subset {\mathbb{Z}}^2\mathrm{with}\left|g\left({\left({\mathbb{Z}}^2\right)}^{\ast }\right)\right|⪇{\aleph }_0$$

(12)

was already referred to in (9) by saying that any continuous self-map satisfying the property (12) does not support the

$\mathit{FPP}$

of

$({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$

. Hence we may consider the following:

Lemma5.

There is no continuous self-map g of $({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$ such that

$$\left\{\begin{array}{l}g\left({\left({\mathbb{Z}}^2\right)}^{\ast }\right)\subset {\mathbb{Z}}^2,\mathit{and}\\ \left|g\left({\left({\mathbb{Z}}^2\right)}^{\ast }\right)\right|={\aleph }_0.\end{array}\right\}$$

(13)

Proof.

Suppose a continuous self-map g of

$({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$

satisfying the property (13). Namely, assume a point

$p\in {\mathbb{Z}}^2$

such that

$g(\ast )=p\in {\mathbb{Z}}^2$

. For convenience, put

$X:=g\left({\left({\mathbb{Z}}^2\right)}^{\ast }\right)$

. Then there is an open set

$S{N}_X\left(p\right):=S{N}_M\left(p\right)\cap X$

(see the just above of Lemma 1) such that

$$\left\{\begin{array}{l}\ast \in g^{-1}\left(S{N}_X\left(p\right)\right)\mathrm{and}\\ |{\left({\mathbb{Z}}^2\right)}^{\ast }\backslash g^{-1}\left(S{N}_X\left(p\right)\right)|⪇{\aleph }_0.\end{array}\right\}$$

Meanwhile, we have

$|X\backslash S{N}_X\left(p\right)|={\aleph }_0$

. Thus the map g should map the finite set

${\left({\mathbb{Z}}^2\right)}^{\ast }\backslash g^{-1}\left(S{N}_X\left(p\right)\right)$

onto the infinite set

$X\backslash S{N}_X\left(p\right)$

, which invokes a contradiction. □

In view of Corollary 3, and Lemmas 4 and 5, and the property (12), we need to prove the following:

Theorem3.

$({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$ has the FPP in $Mop\left({\gamma }^{\ast }\right)$.

Proof.

(Case 1) With the hypothesis, in case g is a constant map, the proof is completed.

(Case 2) Assume an arbitrary morphism g of

$Mop\left({\gamma }^{\ast }\right)$

which is not a constant map. Then we prove that there is a point

$x\in {\left({\mathbb{Z}}^2\right)}^{\ast }$

such that

$g\left(x\right)=x$

. For each morphism

$g:({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })\to ({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$

of

$Mop\left({\gamma }^{\ast }\right)$

, we need to check the following cases.

(Case 2-1) In case

$g(\ast )=\ast$

, which completes the proof.

(Case 2-2) Let us now suppose the morphism g having the property

$g(\ast )\ne \ast$

. Namely, assume the case

$g(\ast )=p\in {\mathbb{Z}}^2$

so that we may consider the following two cases.

(Case 2-2-1) Assume the case

$p\in {\left({\mathbb{Z}}^2\right)}_E$

. Since the set

$\left\{p\right\}$

is compact and closed in

$({\mathbb{Z}}^2,\gamma )$

, it is also closed in

$({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$

. Hereafter, for convenience, put

$g\left({\left({\mathbb{Z}}^2\right)}^{\ast }\right)=X$

. Then, by using the method suggested in Lemma 5, it appears that the point

$p:=(p_1,p_2)$

has

$S{N}_X\left(p\right):=S{N}_M\left(p\right)\cap X$

as a subset of

$\{(p_1\pm 1,p_2),p,(p_1,p_2\pm 1)\}(\subset {\mathbb{Z}}^2)$

(see the property (1)). Owing to the given morphism g, the set

$g^{-1}\left(S{N}_X\left(p\right)\right)(\ni \ast )$

is a denumerable open set in

$({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$

and further,

${\left({\mathbb{Z}}^2\right)}^{\ast }\backslash g^{-1}\left(S{N}_X\left(p\right)\right)$

should be a finite set in

$({\mathbb{Z}}^2,\gamma )$

. Thus the remaining finite set

${\left({\mathbb{Z}}^2\right)}^{\ast }\backslash g^{-1}\left(S{N}_X\left(p\right)\right)$

should be mapped by the map g onto

$X\backslash S{N}_X\left(p\right)$

. Since the set

$X\backslash S{N}_X\left(p\right)$

is infinite, we have a contradiction (see the map g). Namely, the existence of

$S{N}_X\left(p\right)$

such that

$g(\ast )=p\in {\mathbb{Z}}^2$

invokes a contradiction.

(Case 2-2-2) Let us assume the case

$p\in {\left({\mathbb{Z}}^2\right)}_O$

with

$g(\ast )=p$

. Whereas the set

$\left\{p\right\}$

is open in

$({\mathbb{Z}}^2,\gamma )$

, the set

$g^{-1}\left(\left\{p\right\}\right)=\{\ast \}$

is open in

${\gamma }^{\ast }$

containing the point ∗. By using a method similar to the proof of (Case 2-2-1) or Lemma 5 above, we have a contradiction to being a map g.

Based on these cases, we can wrap up that every morphism g of

$({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$

in

$Mop\left({\gamma }^{\ast }\right)$

has the property

$g(\ast )=\ast$

, which leads the FPP of

$({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$

in

$Mop\left({\gamma }^{\ast }\right)$

. □

Example1.

Let us consider any map $g\in Mop\left({\gamma }^{\ast }\right)$. Then, by Lemma 5 and Theorem 3, there is at least the point $\ast \in {\left({\mathbb{Z}}^2\right)}^{\ast }$ such that $g(\ast )=\ast$, which implies that in $Mop\left({\gamma }^{\ast }\right)$, $({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$ has the FPP.

Remark3.

In view of Theorem 2 (in particular, the property (9)), Corollary 3, and Lemmas 4 and 5, the conditions

$Mop\left({\gamma }^{\ast }\right)$

of Theorem 3 cannot be omitted.

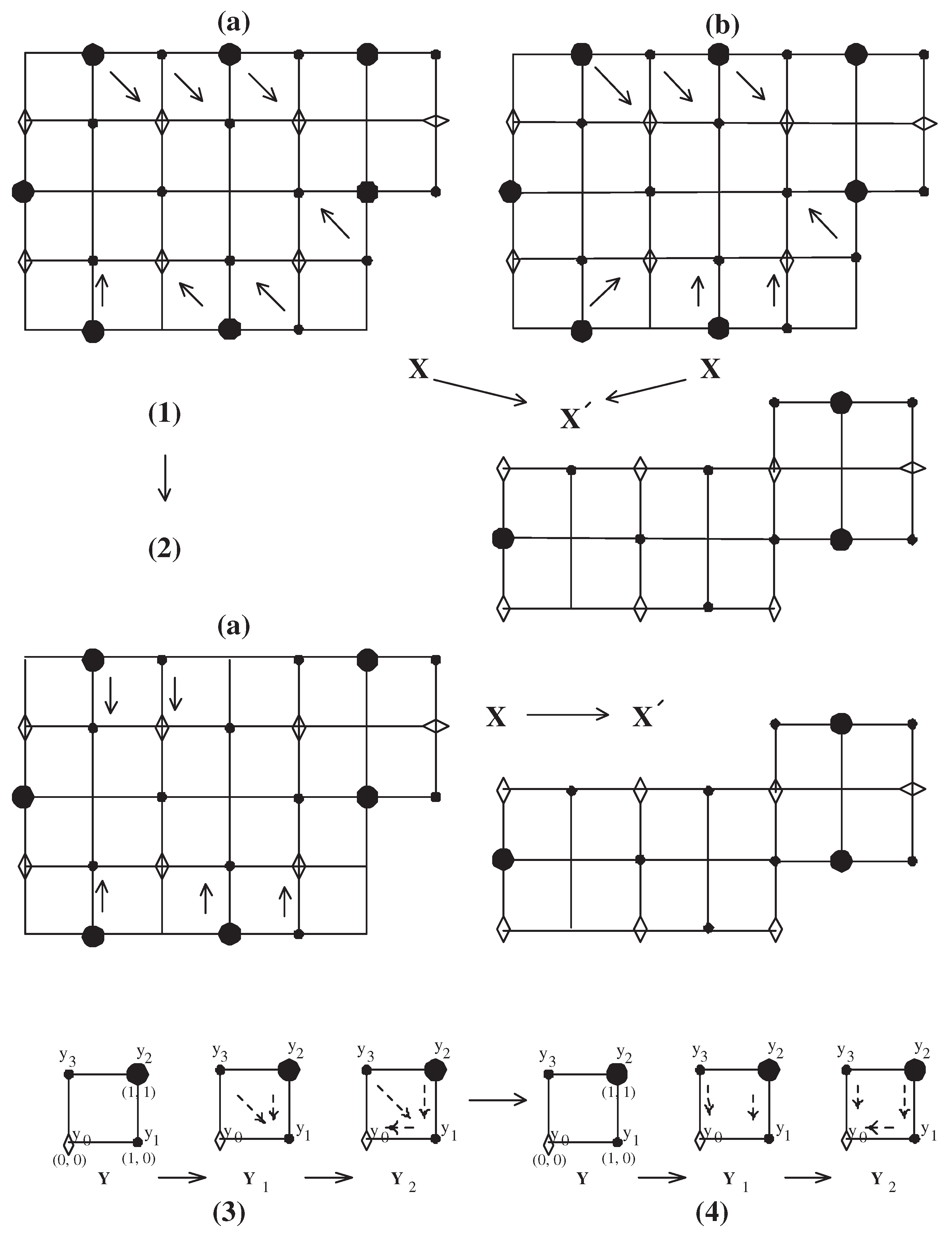
A paper [11] defined the notion of

$MA$

-homotopy (see Definition 11 of [11]) which can be used in applied topology. The definition is correct. In Figure 2a,b of [11] related to Example 4.1(1) of [11], since there was misprinted, let us now make it correct, as follows (see Figure 2 in the present paper):

Example2.

(1) Example 4.1(1) of [11] is written as follows:

Let us consider the space $X\in MAC$ in Figure 2a,b. Then each of the two processes presented by the dotted arrows on the space $X\in MAC$ as in Figure 2(1)a,b represents an $MA$-homotopy of X relative to $X^{\prime }$.

However, there are misprinted figures (a) and (b) for X as shown in Figure 2(1)a,b in the present paper. The corrected one is the following as stated in Figure 2(2)a in the present paper. Using the arrows in Figure 2(2)a in the present paper, we can see an $MA$-homotopy of X relative to $X^{\prime }$.

(2) The picture in Figure 2 of [8] is also misprinted with respect to the dotted arrows. The authors correct it with Figure 2(4) instead of Figure 2(3) (check only the dotted arrows).

In addition, in the configuration of Figure 4c of [16], the word "A K-retractible space" should be written by "A non-K-retractible".

5. Concluding Remarks

After finding the category

$Mop\left({\gamma }^{\ast }\right)$

, we have addressed the unsolved problem: Under what category does

$({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$

have the FPP? Owing to this approach, we conclude that

$Mop\left({\gamma }^{\ast }\right)$

is the maximal category which allows for the FPP of the

$({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$

(see the query (1-5)). Since

$({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$

is one of the digital models for the typical sphere in traditional geometry, this study of

$({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$

facilitate the studies of pure and applied mathematics.

As a further work, based on the tools used in this paper, we can expand the obtained results in this paper to the study of newly-established topology such as the topology on

${\mathbb{Z}}^2$

introduce in the paper [17]. Besides, we can further study the FPP problem for a non-compact, non-Hausdorff, and locally compact Alexandroff plane. In addition, we can adapt this approach into the study of combinatorial topological structures involving digital images [18,19,20]. Motivated by a certain cone metric on a digital image [21,22,23], we can establish a metric space derived from an M-topological space.

Author Contributions

Conceptualization, S.-E.H.; methodology, S.Ö.; validation, S.-E.H. and S.Ö.; formal analysis, S.-E.H.; writing—original draft preparation, S.-E.H.; writing—review and editing, S.-E.H. and S.Ö.; visualization, S.Ö.; supervision, S.-E.H.; project administration, S.-E.H.; funding acquisition, S.-E.H. All authors have read and agreed to the published version of the manuscript.

Funding

The first author was supported by Basic Science Research Program through the National Research Foundation of Korea(NRF) funded by the Ministry of Education, Science and Technology (2019R1I1A3A03059103). In addition, this research was supported by "Research Base Construction Fund Support Program funded by Jeonbuk National University in 2020".

Conflicts of Interest

The authors declare no conflict of interest.

References

1. Han, S.-E. Topologies of the quotient spaces induced by the M-topological plane and the infinite M-topological sphere. Topol. Appl. 2019, 264, 201–209. [Google Scholar] [CrossRef]
2. Han, S.-E.; Na, I.-K. Topologies associated with the one point compactifications of Khalimksy topological spaces. Topol. Appl. 2018, 241, 333–344. [Google Scholar] [CrossRef]
3. Munkres, J.R. Topology a First Course; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 1975. [Google Scholar]
4. Alexandorff, P. Diskrete Räume. Mat. Sb. 1937, 2, 501–518. [Google Scholar]
5. Alexandorff, P.S. Uber die Metrisation der im Kleinen kompakten topologischen Räume. Math. Ann. 1924, 92, 294–301. [Google Scholar] [CrossRef]
6. Marcus, D.; Wyse, F. Solution to problem 5712. Am. Math. Mon. 1970, 77, 1119. [Google Scholar] [CrossRef]
7. Han, S.-E. Generalizations of continuity of maps and homeomorphisms for studying 2D digital topological spaces and their applications. Topol. Appl. 2015, 196, 468–482. [Google Scholar] [CrossRef]
8. Han, S.-E. Almost fixed point property for digital spaces associated with Marcus-Wyse topological spaces. J. Nonlinear Sci. Appl. 2017, 10, 34–47. [Google Scholar] [CrossRef][Green Version]
9. Han, S.-E. Fixed point property for digital spaces. J. Nonlinear Sci. Appl. 2017, 10, 2510–2523. [Google Scholar] [CrossRef][Green Version]
10. Han, S.-E. Homotopic properties of an M A-digitization of 2D Euclidean spaces. J. Comput. Syst. Sci. 2018, 95, 165–176. [Google Scholar] [CrossRef]
11. Han, S.-E.; Yao, W. Homotopy based on Marcus-Wyse topology and its applications. Topol. Appl. 2016, 201, 358–371. [Google Scholar] [CrossRef]
12. Han, S.-E.; Yao, W. An MA-digitization of Hausdorff spaces by using a connectedness graph of the Marcus-Wyse topology. Discret. Appl. Math. 2017, 216, 335–347. [Google Scholar] [CrossRef]
13. Šlapal, J. Digital Jordan curves. Topol. Appl. 2006, 153, 3255–3264. [Google Scholar]
14. Herman, G.T. Oriented surfaces in digital spaces. CVGIP 1993, 55, 381–396. [Google Scholar] [CrossRef]
15. Rosenfeld, A. Digital topology. Am. Math. Mon. 1979, 86, 76–87. [Google Scholar] [CrossRef]
16. Han, S.-E. The fixed point property of non-retractible topological spaces. Mathematics 2019, 7, 879. [Google Scholar] [CrossRef][Green Version]
17. Han, S.-E.; Jafari, S.; Kang, J.M. Topologies on ${\mathbb{Z}}^n$ which are not homeomorphic to the n-dimensional Khalimsky topological space. Mathematics 2019, 7, 1072. [Google Scholar] [CrossRef][Green Version]
18. Kovalevsky, V.A. Finite topology as applied to image analysis. Comput. Vis. Graph. Image Process. 1989, 46, 141–161. [Google Scholar] [CrossRef][Green Version]
19. Latecki, L. Topological connectedness and 8-connectedness in digital pictures. Comput. Vis. Graph. Image Process. 1993, 57, 261–262. [Google Scholar] [CrossRef]
20. Ptak, P.; Kropatsch, V.G. Nearness in digital images and proximity spaces. DGCI:LNCS 2000, 1953, 69–77. [Google Scholar]
21. Aleksić, S.; Kadelburg, Z.; Mitrović, Z.D.; Radenović, S. A new survey: Cone metric spaces. J. Int. Math. Virtual Inst. 2019, 9, 93–121. [Google Scholar]
22. Klen, R.; Manajlović, V.; Simić, S.; Vuorinen, M. Bernoulli inequality and hypergeometric functions. Proc. Am. Math. Soc. 2014, 142, 550–573. [Google Scholar] [CrossRef]
23. Todorć, V. Harmonic Quasiconformal Mapings and Hyperbolic Type Metrics; Springer: Cham, Switzerland, 2019. [Google Scholar]

Figure 1. Configuration of a continuous self-map g of

$({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$

such that

$g\left({\left({\mathbb{Z}}^2\right)}^{\ast }\right)=S{N}_M\left(q\right)$

with the property (9),

$q\in {\left({\mathbb{Z}}^2\right)}_E$

.

Figure 1. Configuration of a continuous self-map g of

$({\left({\mathbb{Z}}^2\right)}^{\ast },{\gamma }^{\ast })$

such that

$g\left({\left({\mathbb{Z}}^2\right)}^{\ast }\right)=S{N}_M\left(q\right)$

with the property (9),

$q\in {\left({\mathbb{Z}}^2\right)}_E$

.

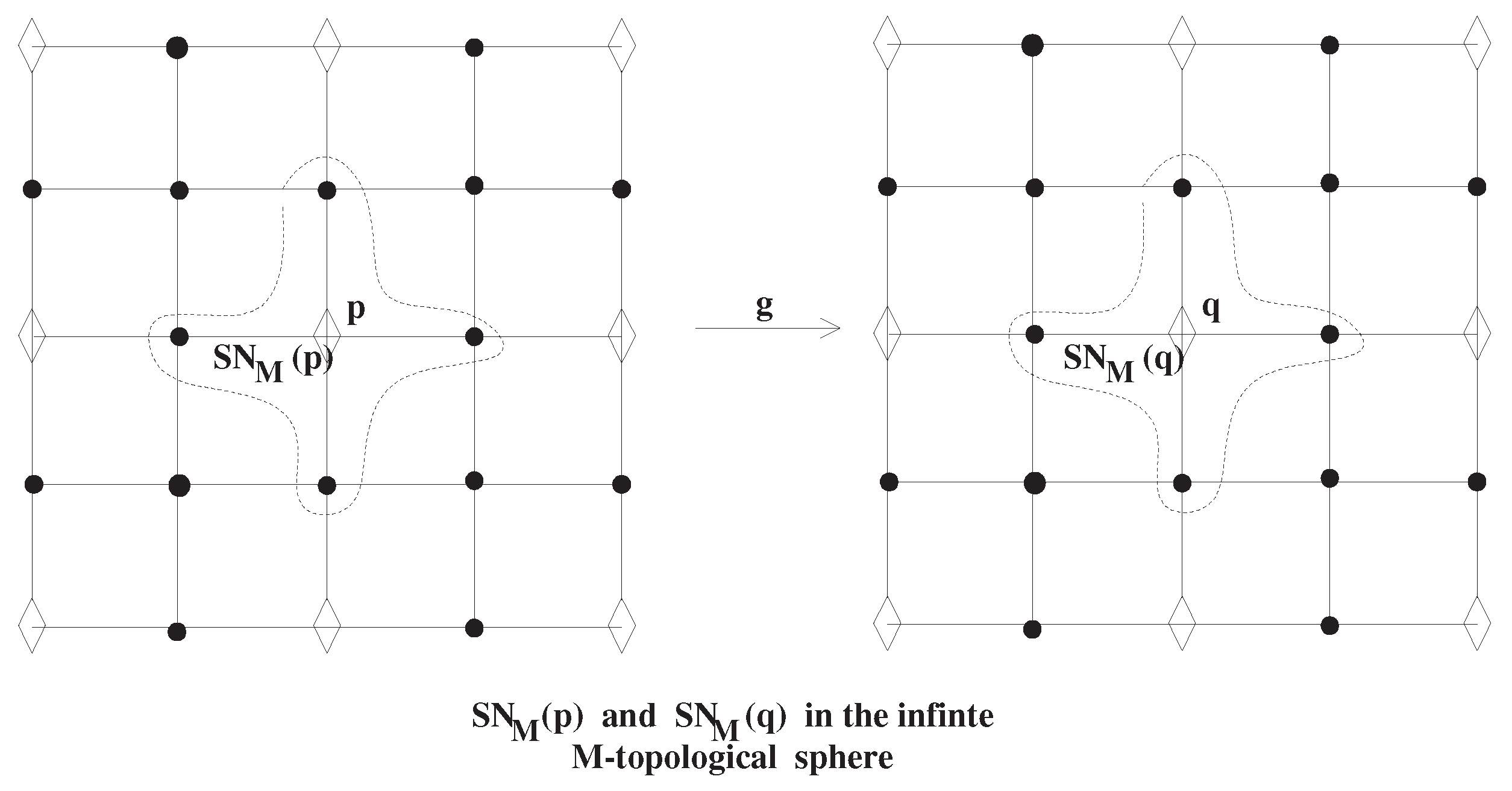
Figure 2. Some corrections of the picture of Figure 4 of [11] and the picture of Figure 2 of [8].

Figure 2. Some corrections of the picture of Figure 4 of [11] and the picture of Figure 2 of [8].

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

isomclook1992.blogspot.com

Source: https://www.mdpi.com/2227-7390/8/4/599/htm

Share this post